Was ist ein Höhenfußpunkt?

Höhenfußpunkt Dreieck

INHALTSANGABE :

INHALTSANGABE

Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persönlichen Lernstatistiken

Jetzt kostenlos anmelden

Nie wieder prokastinieren mit unseren Lernerinnerungen.

Jetzt kostenlos anmelden

In einem Dreieck findest du immer Höhenfußpunkte. Dabei handelt es sich um Punkte, an denen die Höhe eines Dreiecks die zugehörige Seite oder ihre Verlängerung berührt. Der Höhenfußpunkt ist ein Begriff aus der Dreiecksgeometrie.

Als Einleitung findest du hier zunächst eine kleine Wiederholung zum Thema Höhen eines Dreiecks.

Höhen im Dreieck – Wiederholung

Jedes Dreieck im zweidimensionalen Raum hat drei Höhen. Dabei stellt immer eine Dreiecksseite die Grundseite dar, auf die die Höhe aufgestellt wird. Das Lot, das aus dem der Grundseite gegenüberliegenden Punkt auf die Grundseite führt, ist beim spitzwinkligen Dreieck die zugehörige Höhe.

Lies dir dazu gerne noch den Artikel "Höhe Dreieck" durch, wenn du hier noch Auffrischungsbedarf hast.

Höhenfußpunkt Dreieck spitzwinkliges Dreieck Höhe StudySmarter Abbildung 1: Spitzwinkliges Dreieck ABC mit seinen zugehörigen Höhen

Beim stumpfwinkligen Dreieck liegt die Höhe allerdings bei zwei Seiten außerhalb des Dreiecks. Hierbei entspricht die Höhe dem Lot vom der Grundseite gegenüberliegenden Punkt auf die Verlängerung der Grundseite.

Höhenfußpunkt Dreieck stumpfwinkliges Dreieck Höhe StudySmarter Abbildung 2: Stumpfwinkliges Dreieck ABC mit seinen zugehörigen Höhen und den Verlängerungen der Seiten a und c

Bei einem rechtwinkligen Dreieck bildet eine Kathete die Höhe auf die jeweils andere Kathete.

Höhenfußpunkt Dreieck rechtwinkliges Dreieck Höhe StudySmarter Abbildung 3: Rechtwinkliges Dreieck ABC mit seinen zugehörigen Höhen

Höhenfußpunkt Dreieck – Definition

Der Höhenfußpunkt des Dreiecks $H_{x}$ ist der Punkt, an dem die Höhen $h_{x}$ ihre zugehörige Seite $x$ beziehungsweise die Verlängerung der jeweiligen Seite berühren.

Im Folgenden findest du ein Beispiel dazu:

$h_{b}$ ist beispielsweise die Höhe auf die Seite $b$ und damit die Strecke zwischen $B$ und $b$ , die orthogonal zu $b$ steht. Damit ist $H_{b}$ der Höhenfußpunkt der Höhe $h_{b}$ .

Kleine Erinnerung: orthogonal ist gleichbedeutend mit senkrecht, das heißt, der Winkel zwischen Höhe und Seite ist $90 °$ .

Höhenfußpunkt Dreieck spitzwinkliges Dreieck Höhenfußpunkt StudySmarter Abbildung 4: Der Höhenfußpunkt Hb des Dreiecks ABC

Höhenfußpunkt des Dreiecks – Merkmale

Höhenfußpunkt Dreieck Merkmale Erklärung StudySmarter

Der Höhenfußpunkt bildet den Berührungspunkt der Höhe eines Dreiecks und der zugehörigen Seite oder der Verlängerung der zugehörigen Seite.

Der Höhenfußpunkt liegt bei spitzwinkligen und rechtwinkligen Dreiecken immer innerhalb des Dreiecks
- Bei stumpfwinkligen Dreiecken liegen zwei Höhenfußpunkte außerhalb des Dreiecks auf den seitenverlängernden Geraden.

Nicht alle Dreiecksarten haben gleich viele Höhenfußpunkte, obwohl alle Dreiecksarten immer drei unterschiedliche Höhen haben.
- Spitzwinklige Dreiecke und stumpfwinklige Dreiecke haben drei Höhenfußpunkte.
- Rechtwinklige Dreiecke haben nur zwei Höhenfußpunkte, da die beiden Katheten die Höhe für die jeweils andere Kathete bilden. Somit ist der Eckpunkt, an dem beide Katheten und auch der rechte Winkel liegen, der gemeinsame Höhenfußpunkt.

Die Höhenfußpunkte von nicht rechtwinkligen Dreiecken bilden das Höhenfußpunktdreieck.

Die Höhenfußpunkte liegen immer auf dem Feuerbachkreis eines Dreiecks.

Dieser Kreis, auch Neun-Punkte-Kreis genannt, hat auf seiner Kreislinie neun ausgezeichnete Punkte eines Dreiecks.

Höhenfußpunkt Dreieck spitzwinkliges Dreieck Feuerbachkreis StudySmarter Abbildung 5: Der Feuerbachkreis eines spitzwinkligen Dreiecks

Diese Neun Punkte sind

die Mittelpunkte der Seiten $(D, E, F)$ ;
die Höhenfußpunkte $(H_{a}, H_{b}, H_{c})$ ;
die Mittelpunkte der oberen Höhenabschnitte $(K, L, M)$ .

Der obere Höhenabschnitt ist die Strecke zwischen dem Höhenschnittpunkt S und dem jeweiligen Eckpunkt des Dreiecks

Der Feuerbachkreis berührt immer den Inkreis und alle Ankreise eines Dreiecks.

Der Radius des Feuerbachkreises ist immer halb so groß wie der Radius des Umkreises.

Der Kreismittelpunkt G entspricht dem Streckenmittelpunkt der Strecke zwischen dem Umkreismittelpunkt U und dem Höhenschnittpunkt S.

Aufgabe

Konstruiere ein rechtwinkliges und ein gleichseitiges Dreieck und zeichne die zugehörigen Feuerbachkreise ein.

Lösung

Rechtwinkliges Dreieck	Gleichseitiges Dreieck
Abbildung 6: Der Feuerbachkreis des rechtwinkligen Dreiecks geht durch den Scheitel des rechten Winkels	Abbildung 7: Der Feuerbachkreis des gleichseitigen Dreiecks entspricht seinem Inkreis

In der folgenden Tabelle findest du einen Überblick über Höhenfußpunkte bei verschiedenen Dreiecksarten.

Art des Dreiecks	Schema (Abbildungen 8-10)	Anzahl Höhenfußpunkte	Lage der Höhenfußpunkte
Spitzwinkliges Dreieck		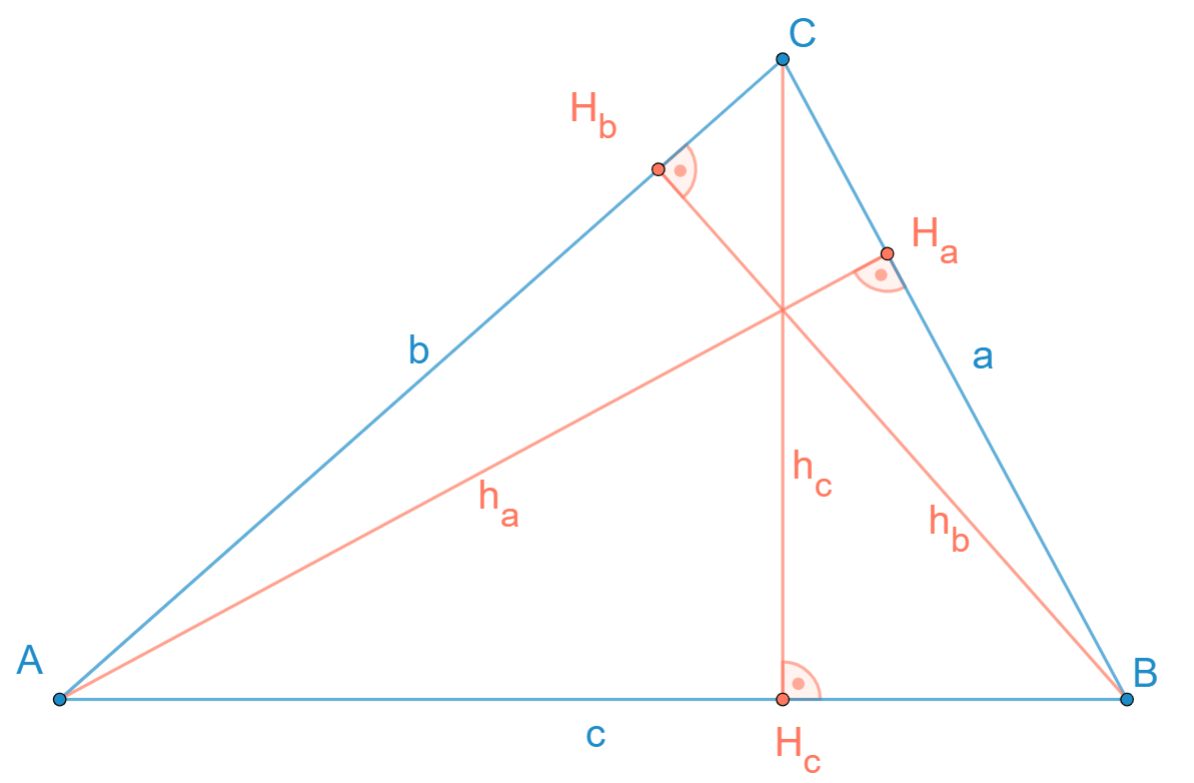3	Auf der zugehörigen Seite
Stumpfwinkliges Dreieck		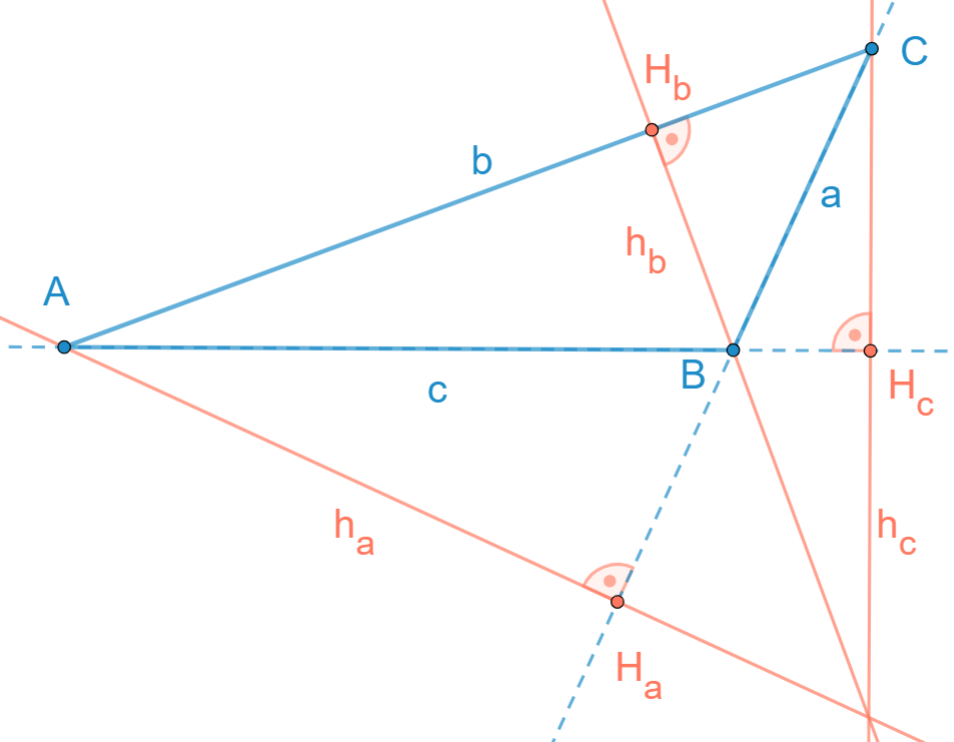3	Bei der längsten Seite auf der zugehörigen Seite; bei den anderen Seiten auf der Verlängerung der zugehörigen Seite
Rechtwinkliges Dreieck		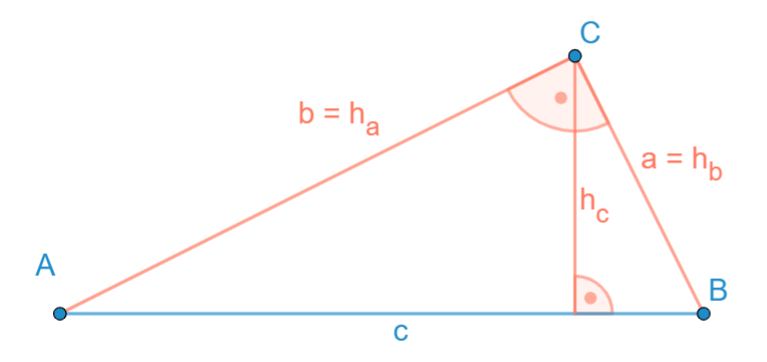2, da die Katheten den gleichen Höhenfußpunkt haben	Bei der Hypotenuse auf der Hypotenuse; bei den Katheten immer der Eckpunkt gegenüber der Hypotenuse

Das Höhenfußpunktdreieck

Bei Dreiecken mit drei Höhenfußpunkten bilden diese ein weiteres Dreieck: das Höhenfußpunktdreieck.

Wie bereits oben angeführt, haben rechtwinklige Dreieck nur zwei unterscheidbare Höhenfußpunkte. Daher können ihre Höhenfußpunkte kein Höhenfußpunktdreieck bilden.

Sieh dir zum Einstieg erst einmal die Definition für das Höhenfußpunktdreieck an:

Das Höhenfußpunktdreieck ist ein Dreieck $H_{a} H_{b} H_{c}$ , das sich aus den Höhenfußpunkten eines Dreiecks $A B C$ ergibt. Die Höhenfußpunkte sind hierbei die Eckpunkte des Höhenfußpunktdreiecks.

Wie diese Punkte im Dreieck aussehen, siehst du im folgenden Beispiel.

In der folgenden Abbildung siehst du das Höhenfußpunktdreieck $H_{a} H_{b} H_{c}$ des Dreiecks $A B C$ :

Höhenfußpunkt Dreieck spitzwinkliges Dreieck Höhenfußpunktdreieck StudySmarter Abbildung 12: Höhenfußpunktdreieck eines spitzwinkligen Dreiecks

Die ersten beiden Eigenschaften betreffen die Innen- beziehungsweise Außenwinkel des Höhenfußpunktdreiecks und ihre Beziehung zu den Höhen des ursprünglichen Dreiecks:

Die Höhen $h_{a}, h_{b}, h_{c}$ des spitzwinkligen Dreiecks ABC bilden die Winkelhalbierenden der Innenwinkel des Höhenfußpunktdreiecks $H_{a} H_{b} H_{c}$ .
Bei stumpfwinkligen Dreiecken halbieren zwei der Höhen des ursprünglichen Dreiecks die Außenwinkel.Die Seiten des ursprünglichen Dreiecks bilden die Winkelhalbierende.Die Dritte Höhe halbiert den Innenwinkel an dem Scheitel des Höhenfußpunktdreiecks, der auf der Seite gegenüber dem stumpfen Winkel des ursprünglichen Dreiecks liegt.

Die dritte Eigenschaft bezieht sich auf den in der oben angesprochenen Vertiefung zum Feuerbachkreis und zum Umkreis des Höhenfußpunktdreiecks:

Der Umkreis des Höhenfußpunktdreiecks entspricht dem Feuerbachkreis des ursprünglichen Dreiecks.

Wenn du nicht mehr genau vor Augen hast, was ein Umkreis oder eine Winkelhalbierende sind, oder was mit Innenwinkel und Außenwinkel gemeint ist, sieh dir einfach noch einmal unsere zugehörigen Artikel an!

Lage der Höhenfußpunkte berechnen

Manchmal kann es vorkommen, dass du ein Dreieck im Koordinatensystem gegeben hast und die Lage zugehöriger Höhenfußpunkte berechnen sollst.

Die Lage des Höhenfußpunktes berechnest du, indem du von einem Punkt außerhalb – dem zugehörigen Scheitelpunkt des Dreiecks – eine Normale an die zugehörige Dreiecksseite anlegst.

Der Schnittpunkt dieser Normalen mit der zugehörigen Dreiecksseite ist der Höhenfußpunkt.

Wenn du dir nicht mehr ganz sicher bist, was eine Normale ist, oder wie man eine Normalengleichung von einem Punkt außerhalb aufstellt, sieh dir gerne nochmal unsere Zusammenfassung zum Thema Normale an.

Bevor du dir die schriftliche Erläuterung zur Berechnung durchliest, sieh dir zunächst die folgende Abbildung an, die das Verfahren veranschaulicht.

Höhenfußpunkt Dreieck Höhenfußpunkt Berechnung StudySmarter Abbildung 11: Verfahren zur Bestimmung der Lage der Höhenfußpunkte

Die Lage des Höhenfußpunktes wird folgendermaßen berechnet:

1. Stelle die Gleichung einer linearen Funktion auf, auf der die zugehörige Dreiecksseite liegt. Nutze dazu die bekannten Dreieckspunkte.

$f (x) = m \cdot x + c$

2. Stelle die allgemeine Normalengleichung zu dieser Funktion auf:

$y = m_{n} \cdot (x - a) + f (a) y = m_{n} \cdot (x - a) + m \cdot a + c$

Dabei gilt:

$m_{n} = - \frac{1}{m}$

3. Setze die Koordinaten des zugehörigen Eckpunktes $S (b | d)$ , durch den die Höhe verläuft, für x und y ein. Nun ist nur noch a unbekannt.

$d = m_{n} \cdot (b - a) + m \cdot a + c$

4. Löst man nun nach a auf und setzt das erhaltene a in die Normalengleichung oder in die zuerst aufgestellte Gleichung, erhält man den Höhenfußpunkt. A entspricht hierbei der x-Koordinate, der errechnete Funktionswert der y-Koordinate:

$H (a | f (a))$

Um das Vorgehen genauer zu verstehen, kannst du dir das folgende Beispiel ansehen.

Aufgabe

Die Punkte $S (0 | 0), B (5 | 0), C (2 | 4)$ bilden ein Dreieck $S B C$ . Bestimme die Lage des Höhenfußpunktes $H_{s}$ , der auf der Seite $s$ liegt.

Lösung

1. Stelle die Gleichung der Geraden auf, die die Seite a beinhaltet:

$f (x) = - \frac{4}{3} \cdot x + \frac{20}{3}$

2. Stelle die zugehörige allgemeine Normalengleichung auf:

$y = \frac{3}{4} \cdot (x - a) - \frac{4}{3} \cdot a + \frac{20}{3}$

3. Setze den Punkt A(0|0) für x und y ein und löse nach a auf:

$\begin{array}{rcl} 0 & = & - \frac{3}{4} \cdot a - \frac{4}{3} \cdot a + \frac{20}{3} \\ \frac{25}{12} a & = & \frac{20}{3} \\ \frac{25}{12} a & = & \frac{80}{12} \\ a & = & \frac{80}{25} = \frac{16}{5} = 3, 2 \end{array}$

4. Setze a=3,2 in die Geradengleichung ein und gib den Höhenfußpunkt an:

$f (3, 2) = 2, 4 H_{s} (3, 2 | 2, 4)$

Die vierte Eigenschaft bezieht sich auf das Fagnano-Problem.

Das Fagnano-Problem beschreibt folgende Schwierigkeit:

Bestimme das in ein Spitzwinkliges Dreieck einbeschriebene Dreieck mit dem geringsten Umfang.

Ein einbeschriebenes Dreieck ist ein Dreieck, das jeweils einen Eckpunkt auf der Seite eines spitzwinkligen Dreiecks hat. Somit liegt es komplett innerhalb des Dreiecks.

Die Lösung des Fagnano-Problems ist das Höhenfußpunktdreieck.

Höhenfußpunkt Dreieck - Das Wichtigste

Ein Höhenfußpunkt ist der Punkt, an dem die Höhe eines Dreiecks die zugehörige Seite oder ihre Verlängerung berührt.
Bei spitzwinkligen Dreiecken liegen alle Höhenfußpunkte innerhalb des Dreiecks, bei stumpfwinkligen Dreiecken liegen zwei Höhenfußpunkte außerhalb.
Höhenfußpunkte haben als ausgezeichnete Punkte eines Dreiecks mehrere Eigenschaften, eine davon ist ihre Lage auf dem Feuerbachkreis.
Die Lage der Höhenfußpunkte berechnet man aus dem Schnittpunkt der linearen Funktion, in der die zugehörige Seite liegt, mit der allgemeinen Normalenfunktion, die durch den zugehörigen Scheitel verläuft.
Die Höhenfußpunkte eines Dreiecks bilden das Höhenfußpunktdreieck, welches die Lösung des Fagnano-Problems darstellt.

Häufig gestellte Fragen zum Thema Höhenfußpunkt Dreieck

Ein Höhenfußpunkt ist der Punkt, an dem die Höhe eines Dreiecks die zugehörige Seite berührt.

Finales Höhenfußpunkt Dreieck Quiz

Höhenfußpunkt Dreieck Quiz - Teste dein Wissen

Frage

Erkläre, was der Höhenfußpunkt eines Dreiecks ist.

Antwort anzeigen

Antwort

Der Höhenfußpunkt eines Dreiecks ist der Schnittpunkt einer Höhe mit der zugehörigen Seite bzw der Verlängerung der zugehörigen Seite bei stumpfwinkligen Dreiecken.

Frage anzeigen

Frage

Wie viele Höhenfußpunkte kann ein Dreieck haben?

Antwort anzeigen

Antwort

Frage anzeigen

Frage

Entscheide, ob die Höhenfußpunkte eines Dreiecks innerhalb des Dreiecks liegen und begründe deine Wahl.

Antwort anzeigen

Antwort

Bei spitzwinkligen und rechtwinkligen Dreiecken liegen alle Höhenfußpunkte innerhalb des Dreiecks, bei stumpfwinkligen Dreiecken lediglich der Höhenfußpunkt der längsten Seite.

Frage anzeigen

Frage

Nenne das Merkmal des Höhenfußpunktdreiecks im Bezug auf Innen- und Außenwinkel.

Antwort anzeigen

Antwort

Spitzwinklige Dreiecke:

Die Höhen des ursprünglichen Dreiecks bilden die Winkelhalbierenden der Innenwinkel des Höhenfußpunktdreiecks

Stumpfwinklige Dreiecke:

Die Höhe auf die längste Seite bildet die Winkelhalbierende des anliegenden Innenwinkels des Höhenfußpunktdreiecks; die Höhen auf die Seitenverlängernden bilden die Winkelhalbierenden des Außenwinkels der anderen beiden Winkel. Hier ist die Seitenverlängernde die Winkelhalbierende des Innenwinkels.

Frage anzeigen

Frage

Beschreibe das bedeutende Merkmal des Umkreises des Höhenfußpunktdreiecks.

Antwort anzeigen

Antwort

Der Umkreis des Höhenfußpunktdreiecks entspricht dem Feuerbachkreis des ursprünglichen Dreiecks.

Frage anzeigen

Frage

Erkläre, wie man die Lage eines Höhenfußpunkts im Koordinatensystem berechnet.

Antwort anzeigen

Antwort

Zunächst stellt man eine Geradengleichung auf, die die Seite des zu berechnenden Höhenfußpunkts abbildet. Dann stellt man mithilfe der allgemeinen Normalengleichung eine Normale zu dieser Gerade auf, die durch den Punkt gegenüber der Seite geht. Diese Normale bildet die Höhe ab. Der Schnittpunkt der Geraden mit ihrer Normale ist der Höhenfußpunkt.

Frage anzeigen

Frage

Erläutere, warum ein rechtwinkliges Dreieck nur 2 Höhenfußpunkte hat.

Antwort anzeigen

Antwort

Die beiden Katheten bilden die Höhe auf die jeweils andere. Damit ist der Dreieckspunkt zwischen den Katheten auch gleichzeitig ein doppelter Höhenfußpunkt. Der zweite Höhenfußpunkt liegt auf der Hypotenuse.

Frage anzeigen

Frage

Nenne die ausgezeichneten Punkte im Dreieck, die auf dem Feuerbachkreis liegen.

Antwort anzeigen

Antwort

Auf dem Feuerbachkreis liegen die Höhenfußpunkte, die Mittelpunkte der Seiten und die Mittelpunkte der oberen Höhenabschnitte.

Frage anzeigen

Frage

Gib an, wo sich der Mittelpunkt des Feuerbachkreises befindet.

Antwort anzeigen

Antwort

Der Mittelpunkt des Feuerbachkreises ist der Streckenmittelpunkt der Strecke zwischen Höhenschnittpunkt und Umkreismittelpunkt.

Frage anzeigen

Karteikarten in Höhenfußpunkt Dreieck9

Lerne jetzt

Erkläre, was der Höhenfußpunkt eines Dreiecks ist.

Der Höhenfußpunkt eines Dreiecks ist der Schnittpunkt einer Höhe mit der zugehörigen Seite bzw der Verlängerung der zugehörigen Seite bei stumpfwinkligen Dreiecken.

Wie viele Höhenfußpunkte kann ein Dreieck haben?

Entscheide, ob die Höhenfußpunkte eines Dreiecks innerhalb des Dreiecks liegen und begründe deine Wahl.

Bei spitzwinkligen und rechtwinkligen Dreiecken liegen alle Höhenfußpunkte innerhalb des Dreiecks, bei stumpfwinkligen Dreiecken lediglich der Höhenfußpunkt der längsten Seite.

Nenne das Merkmal des Höhenfußpunktdreiecks im Bezug auf Innen- und Außenwinkel.

Spitzwinklige Dreiecke:

Die Höhen des ursprünglichen Dreiecks bilden die Winkelhalbierenden der Innenwinkel des Höhenfußpunktdreiecks

Stumpfwinklige Dreiecke:

Beschreibe das bedeutende Merkmal des Umkreises des Höhenfußpunktdreiecks.

Der Umkreis des Höhenfußpunktdreiecks entspricht dem Feuerbachkreis des ursprünglichen Dreiecks.

Erkläre, wie man die Lage eines Höhenfußpunkts im Koordinatensystem berechnet.

Lerne mit 9 Höhenfußpunkt Dreieck Karteikarten in der kostenlosen StudySmarter App

Mit E-Mail registrieren ANMELDEN ANMELDEN

Du hast bereits ein Konto? Anmelden

Finde Lernmaterialien und -tipps

Erstelle Lernmaterialien

Blog

Select your language

Höhenfußpunkt Dreieck

Höhen im Dreieck – Wiederholung