Wusstest du, dass die gestrichelte Farbbahnmarkierung in der Mitte einer geraden Straße eine Mittelparallele darstellt? Und wieso? Das sehen wir uns gemeinsam an.
Die Mittelparallele ist genauso wie die Kreislinie, die Winkelhalbierende, die Mittelsenkrechte und ein Parallelenpaar ein geometrischer Ort.
Zur Erinnerung: Ein geometrischer Ort ist eine Menge von Punkten, die eine gewisse Bedingung erfüllen.
Mittelparallele Definition
Die Mittelparallele ist eine Gerade, die zwischen zwei parallelen Geraden – also zwischen einem Parallelenpaar – liegt und zu beiden Geraden parallel ist. Sie schneidet also die Geraden nie, zwischen denen sie liegt.
Auf der Mittelparallele liegen also alle Punkte, die denselben Abstand zum Parallelenpaar haben.
Daher kann man die Mittelparallele als geometrischer Ort wie folgt definieren:
Die Mittelparallele m des Parallelenpaares g und h ist die Menge aller Punkte aus der Ebene, die denselben Abstand d zu g und zu h haben, für die gilt: .
Abbildung 1: Mittelparallele m zum Parallelenpaar g und h
Es gibt noch eine weitere Definition der Mittelparallelen als geometrischen Ort. Sie ist die Menge aller Mittelpunkte von Kreisen, die die Geraden g und h berühren, sie aber nicht schneiden.
Abbildung 2: Definition der Mittelparallele als geometrischer Ort
Super, damit weißt du bereits, was genau eine Mittelparallele ist. Sehen wir uns als Nächstes an, wie wir sie zusammen zeichnen können.
Mittelparallele konstruieren zwei Geraden
Mithilfe eines Zirkels und eines Lineals lässt sich die Mittelparallele in wenigen Schritten konstruieren. Gern kannst du mithilfe der folgenden Anleitung direkt selbst eine Mittelparallele zeichnen!
Hinweis: Für die Konstruktion der Mittelparallele solltest du wissen, wie man eine Mittelsenkrechte konstruiert und ein Lot fällt. Das kannst du in unserer Zusammenfassung zum Thema Mittelsenkrechte konstruieren nachlesen!
| Konstruktionsbeschreibung | Konstruktionsbild |
| Gegeben ist ein Parallelenpaar, bestehend aus den Geraden g und h. | 
Abbildung 3: Erster Schritt der Konstruktion |
Wähle einen beliebigen Punkt P auf der Geraden g.Du könntest auch einen Punkt auf der Geraden h wählen, das macht keinen Unterschied für die Konstruktion. | 
Abbildung 4: Zweiter Schritt der Konstruktion |
| Fälle nun das Lot durch den Punkt P auf die Gerade g. Du erhältst nun auch einen Schnittpunkt des Lots und der Geraden h, welchen wir S nennen. Ein Lot kannst du mit deinem Geodreieck aufstellen. | 
Abbildung 5: Vorletzter Schritt zur Konstruktion |
Konstruiere nun die Mittelsenkrechte m der Strecke  . Sie ist die gesuchte Mittelparallele m zu den Geraden g und h. Hierbei kann dir wieder dein Geodreieck helfen. | 
Abbildung 6: Letzter Schritt zur Konstruktion |
Mittelparallele Trapez berechnen
Vielleicht hast du bereits von der Mittelparallelen eines Trapezes gehört. Man nennt sie manchmal auch Mittellinie.
Die Mittelparallele m eines Trapezes ist eine Strecke, welche parallel zu den beiden parallelen Seiten a und c des Trapezes verläuft und deren Anfangs- und Endpunkt die Mittelpunkte und der anderen beiden Seiten b und d sind.
Abbildung 7: Mittelparallele eines Trapez
Die Mittelparallele eignet sich beispielsweise zur Berechnung des Flächeninhalts des Trapezes.
Wenn du wissen möchtest, wie man die Mittellinie zur Berechnung des Flächeninhalts eines Trapezes nutzen kann, dann solltest du dir den Artikel Flächeninhalt Trapez anschauen.
Um nun die Länge der Mittelparallele bzw. Mittellinie zu berechnen, kannst du die folgende Formel verwenden:
Formel zur Berechnung der Mittellinie m in einem Trapez :
Schau dir die Verwendung der Formel am besten am folgenden Beispiel an:
Aufgabe 1
Gegeben sei das Trapez , wobei die parallelen Seiten a und c sind, mit und .
Berechne die Länge der Mittelparallele m.
Lösung
Es müssen lediglich die Längen der Seiten a und c in die Formel eingesetzt werden:
Die Mittellinie m ist also lang.
Abbildung 8: Mittelparallele des Trapezes
Mittelparallele Dreieck
Auch im Dreieck gibt es Mittelparallelen, insgesamt drei Stück. Sie verlaufen jeweils parallel zu einer Seite und ihre Anfangs- und Endpunkte sind die Mittelpunkte der beiden anderen Seiten.
Abbildung 9: Mittelparallele eines Dreiecks
Sie umschließen zudem ein Dreieck, welches zum Dreieck ABC ähnlich ist.
Falls du nicht mehr genau weißt, was "ähnlich" bedeutet, kannst du dir den Artikel "Ähnlichkeit" anschauen!
Es gibt sogar einen Satz der Mittelparallelen im Dreieck. Dieser besagt, dass die Strecke durch die Mittelpunkte zweier Seiten eines Dreiecks stets parallel zur dritten Seite ist - egal um welche Art von Dreieck es sich handelt.
Mittelparallele Übung
Um die in diesem Artikel gelernten Inhalte ein bisschen zu festigen, kannst du die folgende Aufgabe bearbeiten.
Aufgabe 2
Berechne die Länge der Mittelparallele eines Trapezes mit den folgenden Seitenlängen:
1.
2.
3.
Dabei sind a und c die beiden parallelen Seiten des Trapezes.
Lösung
1. Wir können die beiden Werte direkt in die gegebene Formel einsetzen:
2. Auch hier können wir die Formel nutzen:
3. Hier müssen wir ein bisschen aufpassen, denn: Die gegebenen Seitenlängen sind nicht in der gleichen Einheit! Es bietet sich an, beide Längen in die Einheit cm umzuwandeln:
Nun können wir aber wieder die Formel verwenden:
Befindest du dich bereits in der Oberstufe und hast die Mittelparallele im dreidimensionalen Raum betrachtet, so kannst du dir ebenfalls unsere Vertiefung zu diesem Thema ansehen.
Die Mittelparallele zweier Geraden im Dreidimensionalen
Sind zwei parallele Geraden im dreidimensionalen Koordinatensystem gegeben, so kann man eine Gleichung für die Mittelparallele m berechnen. Wie das funktioniert, soll an einem Beispiel verdeutlicht werden.
Gegeben seien die Geraden 
und 
, 
Zeige, dass g und h parallel sind und berechne die Mittelparallele m.
Wenn du nicht mehr weißt, wie man die gegenseitige Lage zweier Geraden im dreidimensionalen Raum überprüft, dann solltest du in den Artikel "Gegenseitige Lage von Geraden" schauen!
| Erläuterung | Rechnung |
Um zu überprüfen, ob g und h parallel sind, wird als Erstes überprüft, ob die beiden Richtungsvektoren in den Geradengleichungen linear abhängig oder linear unabhängig sind.Sind die Richtungsvektoren linear abhängig, dann können die Geraden entweder identisch oder parallel sein. | Die beiden Richtungsvektoren sind linear abhängig, denn: |
| Dann wird die sogenannte Punktprobe gemacht, also überprüft, ob der Aufpunkt der Geraden g auf der Gerade h liegt.Liegt der Aufpunkt auf der Geraden h, so sind g und h identisch. Liegt er nicht auf h, so sind g und h parallel. Diesen Fall brauchen wir, um eine Mittelparallele bestimmen zu können. | Diese Gleichung hat keine Lösung. Es folgt also: |
| Nun wird die Mittelparallele berechnet:Da m parallel zu g und h sein soll, muss ihr Richtungsvektor linear abhängig zu den Richtungsvektoren von g und h sein. Der Einfachheit halber bietet es sich an, einfach den Richtungsvektor von g oder h zu nutzen. | Wähle zum Beispiel den Richtungsvektor der Geraden g: ,  |
| Zuletzt muss ein Punkt gefunden werden, der genau zwischen den Geraden g und h liegt.Ein möglicher Punkt, der sich leicht berechnen lässt, ist der Mittelpunkt der Strecke zwischen den Aufpunkten der Geraden g und h. | |
| Damit haben wir die Mittelparallele berechnet. |  ,  |
Auch im Dreidimensionalen lassen sich die Geraden und die Mittelparallele darstellen. In der Abbildung 10 sind alle geometrischen Objekte noch einmal eingezeichnet.
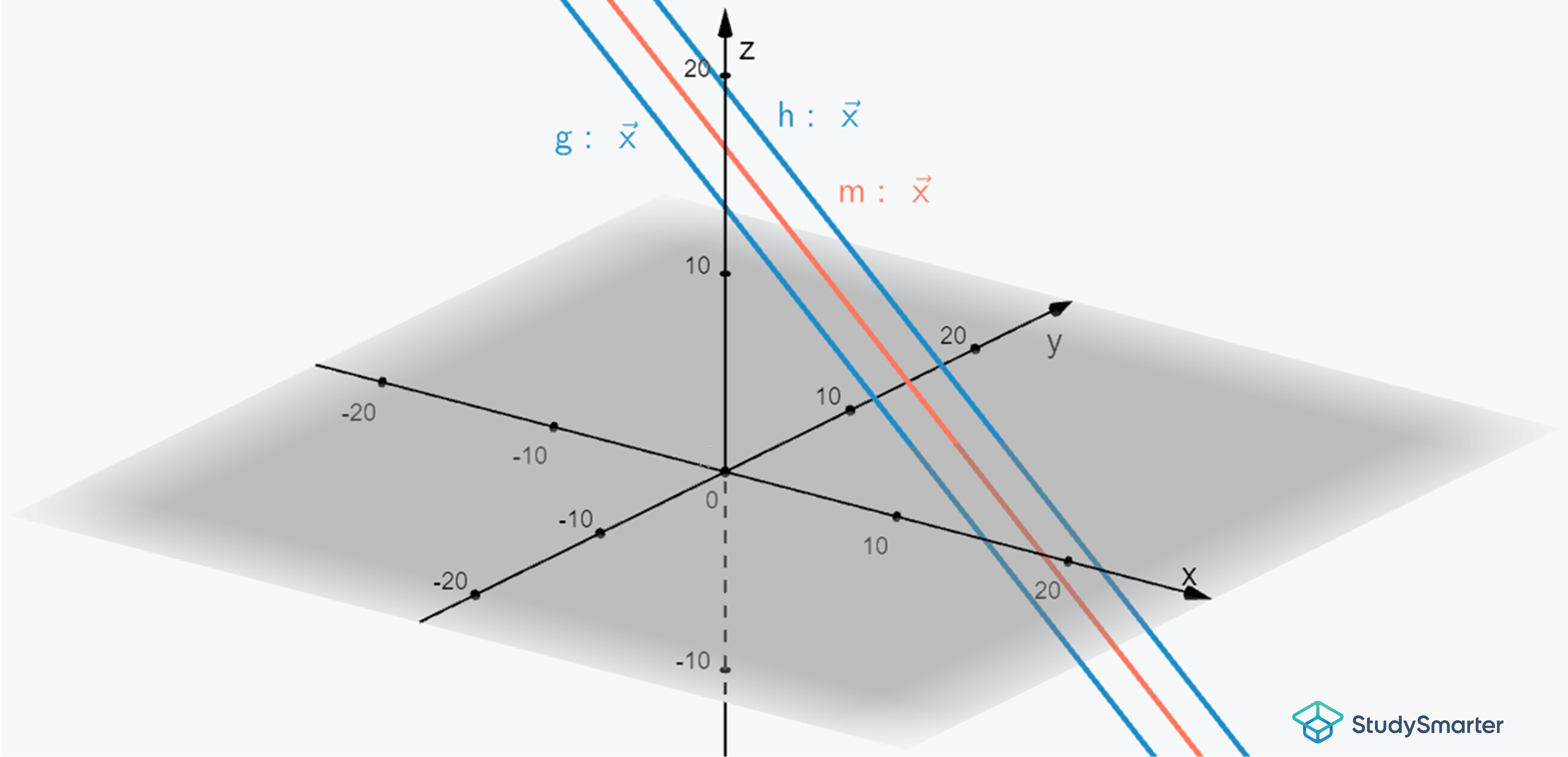
Abbildung 10: Geraden und Mittelparallele in 3D
Zusammenfassend noch einmal die Schritte zur Berechnung der Mittelparallele zweier Geraden im dreidimensionalen Koordinatensystem:
- Prüfe, ob die gegebenen Geraden wirklich parallel sind. Dazu müssen die Richtungsvektoren linear abhängig sein und der Aufpunkt der einen Gerade darf nicht auf der anderen Gerade liegen.
- Berechne den Mittelpunkt M zwischen den beiden Aufpunkten der parallelen Geraden.
- Wähle als Richtungsvektor der Mittelparallelen den Richtungsvektor einer der parallelen Geraden.
Um diese Schritte einzuüben, gibt es auch hier noch eine Übungsaufgabe für dich:
Aufgabe
Überprüfe die Lage der folgenden Geraden und berechne die Mittelparallele.
und 
, 
Lösung
Schritt 1:
g und h sind parallel, denn ihre Richtungsvektoren sind linear abhängig:
Außerdem liegt der Aufpunkt der Geraden g nicht auf der Geraden h, denn die Punktprobe hat keine Lösung in 
:
Schritt 2:
Der Mittelpunkt der Strecke zwischen den beiden Aufpunkten lässt sich berechnen durch:
Schritt 3:
Mit einem der Richtungsvektoren von g oder h ergibt sich für die Mittelparallele die folgende Gleichung:
Mittelparallele - Das Wichtigste
- Die Mittelparallele m des Parallelenpaares g und h ist die Menge aller Punkte aus der Ebene, die denselben Abstand zu g und zu h haben.
- Im Zweidimensionalen kann man die Mittelparallele mithilfe von einem Geodreieck und einem Zirkel konstruieren.
- Jedes Trapez hat eine Mittelparallele. Mit deren Länge kann man den Flächeninhalt berechnen.
- Im Dreieck gibt es drei Mittelparallelen.
- Für Mathe-Experten: Zu zwei parallelen Geraden im dreidimensionalen Raum kann man die Mittelparallele berechnen.
Erklärungen 
Magazine 
