
Zufallsexperimente
Ohne es zu wissen, hast du sicher bereits schon selbst Zufallsversuche durchgeführt. Das kann beispielsweise ein Münzwurf sein oder auch das Würfeln eines Würfels. Weißt du noch, wie solche Experimente mathematisch definiert sind?
Allgemeines Zufallsexperiment

Der Wurf eines Würfels ist ein klassisches Zufallsexperiment.
Mathematisch können wir dies wie folgt definieren:
Ein Versuch mit mehreren möglichen zufälligen Ausgängen wird als Zufallsexperiment bezeichnet. Es gilt:
In der Ergebnismenge werden alle möglichen Versuchsausgänge (=Ergebnisse) des Zufallsexperiments zusammengefasst. Die Einzelergebnisse werden auch als Elementarereignis bezeichnet. Möglich ist dabei auch, einzelne Elementarereignisse zu einer Teilmenge A, dem sogenannten Ereignis, zusammenzufassen.
Mehr Informationen zu einem Zufallsexperiment findest du in dem Artikel Zufallsexperimente / Zufallsversuch auf StudySmarter.
Und was genau ist jetzt ein Bernoulli-Experiment?
Das Bernoulli-Experiment
Ein Würfelwurf kann sechs mögliche Ausgänge liefern, nämlich die Augenzahl 1 bis 6 des Würfels. Dies ist kein Bernoulli-Experiment, da ein Bernoulli-Experiment eine Besonderheit aufweist:
Ein Zufallsexperiment mit nur zwei möglichen Ausgängen wird als Bernoulli-Experiment bezeichnet. Die Ereignisse werden meist mit "Erfolg" und "Misserfolg" oder "Treffer" und "Niete" deklariert.
Das Bernoulli-Experiment geht übrigens zurück auf den Schweizer Mathematiker Jakob Bernoulli (1655–1705).
Das Zufallsexperiment eines Würfelwurfs liefert sechs verschiedene Ausgänge.
Dies entspricht demnach nicht der Definition eines Bernoulli-Experiments. Es wäre aber möglich, das Zufallsexperiment eines Würfels so abzuwandeln, dass wir doch noch ein Experiment nach Bernoulli erhalten. Wie? Sehen wir uns das zusammen an.
Wir wollen eine Augenzahl von 3 würfeln. Theoretisch wären wieder die Zahlen 1 bis 6 möglich. Jedoch bewerten wir den Ausgang dieses Wurfs lediglich danach, ob eine 3 gewürfelt wurde oder nicht. Es gilt demnach:

Wir würfeln eine 4. Was bedeutet das für unser Experiment? Hatten wir Erfolg? Nein, leider nicht, denn wir brauchen eine Würfelzahl von 3. Wir müssen den Versuchsausgang daher als Misserfolg werten.
Wenn du dieses wichtige Kriterium schon verinnerlicht hast, dann hast du bereits den Kernpunkt eines
Bernoulli-Experimentes kennengelernt. Schauen wir uns das Ganze doch mal anhand eines weiteren Beispiels für ein Bernoulli Experiment an.
In der Schule wird mit einem Eimer mit Losen durchgegangen. Du darfst dabei ein Los ziehen. Es gibt entweder ein Gewinn oder eine Niete.
 Abbildung 1: Lose
Abbildung 1: Lose
Dies ist ein klassischer Fall für ein Bernoulli-Experiment, denn wir haben nur zwei Ausgänge. Entweder ein Gewinn oder eine Niete. Dies können wir wieder im Ergebnisraum darstellen:
Sobald wir ein drittes Ereignis haben, wie zum Beispiel noch ein zusätzliches Los für den Hauptgewinn, den man ziehen kann, handelt es sich nicht mehr um ein Bernoulli-Experiment.
Ein Bernoulli-Experiment darf also nur zwei mögliche Ausgänge besitzen.
Noch mehr Infos zum Thema Bernoulli-Experiment erwünscht? Kein Problem. Lies einfach mehr dazu im entsprechenden Artikel.
Was jetzt aber für Beschreibung eines solchen Experiments noch fehlt, ist die Frage, wie wahrscheinlich ein Ereignis eintrifft. Wie wahrscheinlich ist es denn, beispielsweise eine Augenzahl von 3 zu würfeln oder nicht?
Wahrscheinlichkeiten und Zufallsvariable
Die Wahrscheinlichkeiten geben bei einem Zufallsexperiment Auskunft darüber, wie wahrscheinlich ein Ereignis eintritt oder nicht.
Wahrscheinlichkeiten eines Bernoulli-Experiments
Wir haben bereits Lose gezogen und gewürfelt, uns jedoch nicht gefragt, wie wahrscheinlich es eigentlich ist, dass wir beispielsweise eine Würfelzahl von 3 erhalten. Am einfachsten lassen sich solche Wahrscheinlichkeiten mithilfe eines Baumdiagramms erklären. Sehen wir uns dazu ein weiteres Beispiel an.
Dieses Mal werfen wir eine Münze in die Luft und warten darauf, welche Seite nach dem Fallen auf der Oberseite der Münze zu sehen ist.

Möglich sind nur zwei Ausgänge: Kopf oder Zahl. Damit ist dies ein klassisches Bernoulli-Experiment.
Wie wahrscheinlich ist es in diesem Versuch, dass wir als Ergebnis Kopf oder Zahl erhalten? Das lässt sich leicht mit einem Baumdiagramm ermitteln.
 Abbildung 1: Baumdiagramm
Abbildung 1: Baumdiagramm
Da nur zwei Ergebnisse möglich sind, haben wir eine 50%ige Chance, Kopf zu werfen. Demnach gilt eine Trefferwahrscheinlichkeit für Kopf. Diese ist in einem Baumdiagramm neben dem Pfad gekennzeichnet. Für Zahl erhalten wir ebenfalls eine Gegenwahrscheinlichkeit q von:
Mit der Trefferwahrscheinlichkeit p können wir unsere Wahrscheinlichkeit und berechnen:
Würden wir diesen Wurf wiederholen, dann gilt ebenfalls wieder eine 50 % Chance Kopf oder Zahl zu werfen. Wir können demnach das Baumdiagramm erweitern.
 Abbildung 4: Baumdiagramm Bernoulli-Kette
Abbildung 4: Baumdiagramm Bernoulli-Kette
Hier handelt es sich jetzt um eine Bernoulli-Kette, denn wir haben das Bernoulli-Experiment wiederholt. Egal, wie oft wir diesen Versuch wiederholen, die Trefferwahrscheinlichkeit p, dass wir Kopf werfen, wird sich aber nicht verändern.
Sind dir die Pfadregeln eines Baumdiagramms nicht mehr ganz klar? Dann lies einfach im entsprechenden Kapitel auf StudySmarter nach.
Mathematisch können wir die Wahrscheinlichkeiten des Bernoulli-Experiments wie folgt zusammenfassen und definieren:
Als Trefferwahrscheinlichkeit wird die Wahrscheinlichkeit p definiert, mit der der Ausgang A (Erfolg, Treffer) eintritt. Die Gegenwahrscheinlichkeit q eines Ausgangs (Misserfolg, kein Treffer) ist:
Bleiben die Wahrscheinlichkeiten eines Bernoulli-Experiments durch n-fache Wiederholung gleich, so kann dies als Bernoulli-Kette bezeichnet werden mit:
Für die Wahrscheinlichkeit P eines Erfolgs A und eines Misserfolgs eines Bernoulli-Experiments gilt:
Die Wahrscheinlichkeiten eines Bernoulli-Experiments haben wir damit bereits ermittelt. Sehen wir uns zunächst noch die Zufallsgröße an.
Zufallsgröße eines Bernoulli-Experiments
Rechnen lässt es sich mit Wörtern oder Symbolen schlecht. Unsere Ergebnisse in der Ergebnismenge haben wir bisher mit Worten beschrieben wie "Erfolg" oder "Misserfolg". In der Mathematik ist es aber von Vorteil, solche Ergebnisse einer reellen Zahl x zuzuordnen. Dazu gibt es die sogenannte Zufallsgröße oder Zufallsvariable X.
In der Literatur findest du häufig auch die Bezeichnungen Zufallsgröße Y oder Zufallsgröße Z.
Definiert wird sie formal wie folgt:
Als Zufallsgröße oder Zufallsvariable X wird eine Funktion bezeichnet, die jedem Ergebnis in der Ergebnismenge eine reelle Zahl x zuordnet. Es gilt:
mit
Für das Bernoulli-Experiment lassen sich ebenfalls reelle Zahlen zuordnen, für Erfolg und Misserfolg.
Zufallsvariable X eines Bernoulli-Experiments:
Die Zufallsvariable X ist Bernoulli-verteilt mit den Parametern :
Demnach ordnen wir der Zufallsvariable X in einem Bernoulli-Experiment nur die Werte 1 und 0 zu, da wir nur zwei verschiedene Ausgänge erhalten können. Die Bernoulli-Verteilung wird manchmal deshalb auch
Null-Eins-Verteilung, alternativ Verteilung oder Boole-Verteilung genannt.
Mit diesem Wissen zu den Größen des Bernoulli-Experiments lassen sich verschiedene Funktionen ermitteln.
Wahrscheinlichkeitsfunktion einer bernoulliverteilten Zufallsgröße
Wie du bereits gesehen hast, können wir den Ergebnissen des Experiments verschiedene Wahrscheinlichkeiten zuordnen. Erweitern wir diese Formeln, so erhalten wir eine Wahrscheinlichkeitsfunktion f(x). Sie ordnet jedem Wert einer Zufallsvariable X eine Wahrscheinlichkeit P zu.
Diese Funktion lässt sich auch graphisch abbilden. Dabei existieren mehrere Darstellungsmöglichkeiten:
Lass uns diese Möglichkeiten an einem Beispiel zeigen.
Wir wissen ja bereits, dass wir bei einer Tombola die Möglichkeiten haben, einen Gewinn oder eine Niete zu ziehen. Vereinfachen wir die Aufgabenstellung, indem wir von insgesamt 10 Losen ausgehen, wobei nur ein einziger Gewinn dabei ist.
Damit liegt die Trefferwahrscheinlichkeit p für einen Gewinn bei und die für eine Niete bei . Die Wahrscheinlichkeiten P berechnen sich durch:
Allgemein lautet die Wahrscheinlichkeitsfunktion für diesen Fall:
Setzen wir nun die Zahlenwerte von oben ein, so erhalten wir:
Wir erstellen dazu die drei verschiedenen Diagramme.
 Abbildung 6: Verteilung in verschiedenen Diagrammen
Abbildung 6: Verteilung in verschiedenen Diagrammen
Sehen wir uns zur Übung noch ein weiteres Beispiel an.
Wir haben eine Urne mit 5 Kugeln, wobei davon 2 türkis und 3 orange sind. Im Experiment ziehen wir einmal. Dabei betrachten wir das erfolgreiche Ziehen einer orangen Kugel als Erfolg und das Nichtziehen dieser Farbe als Misserfolg.
 Abbildung 7: Kugeln in Urne
Abbildung 7: Kugeln in Urne
Die Wahrscheinlichkeiten P für das Ziehen einer orangen Kugel liegen bei:
Auch dieses Mal können wir die Wahrscheinlichkeitsfunktion f(x) für das Ziehen einer orangen Kugel aufstellen und anschließend in ein Histogramm einzeichnen:
Würden wir das Ziehen einer türkisen Kugel als Erfolg ansehen, dann drehen sich die Wahrscheinlichkeiten um. Im folgenden Diagramm sind beide Varianten eingezeichnet.
 Abbildung 8: Wahrscheinlichkeitsfunktion f(x) im Diagramm
Abbildung 8: Wahrscheinlichkeitsfunktion f(x) im Diagramm
Übrigens: Sind die Wahrscheinlichkeiten für alle Ergebnisse gleich groß, dann handelt es sich zudem auch um ein Laplace-Experiment. Mehr dazu kannst du im entsprechenden Kapitel nachlesen.
Bei der Wahrscheinlichkeitsverteilung sind alle zutreffenden Wahrscheinlichkeiten einzeln betrachtet worden. Teilweise benötigt man aber auch zusammengesetzte Wahrscheinlichkeiten. Diese lassen sich mithilfe der Verteilungsfunktion F(x) darstellen.
Verteilungsfunktion einer bernoulliverteilten Zufallsgröße
Die sogenannte kumulative Verteilungsfunktion F(x) gibt an, wie groß die Wahrscheinlichkeit ist, dass das Ergebnis kleiner oder gleich x ist. Es ist eine Treppenfunktion mit Sprüngen in einer bestimmten Höhe. Was genau heißt das? Sehen wir es uns zusammen an.
Allgemein gilt für das Bernoulli-Experiment:
Verteilungsfunktion eines Bernoulli-Experiments:
Damit du gleich ein besseres Verständnis für die Verteilungsfunktion F(x) eines Bernoulli-Experiments erhältst, sehen wir uns direkt ein Beispiel an.
Wir betrachten wieder unser Beispiel mit den türkisen und orangen Kugeln in einer Urne. Drei der Kugeln sind orange und zwei Kugeln sind türkis.
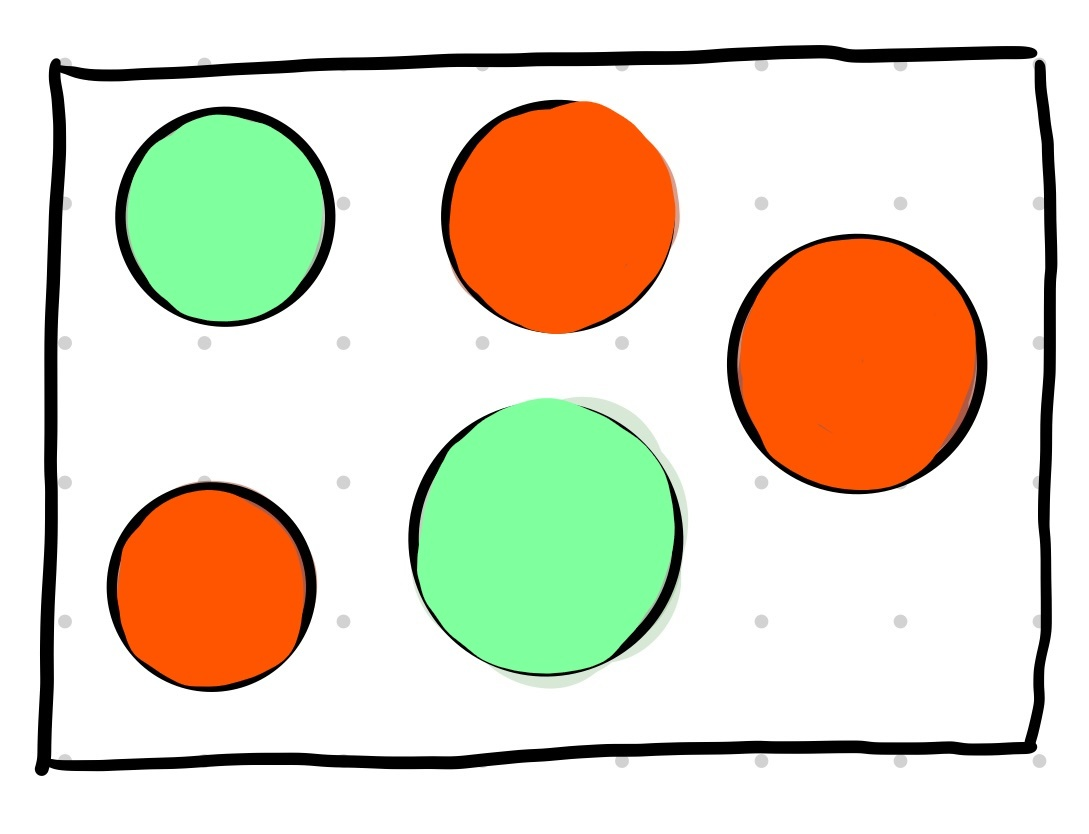
Abbildung 9: Kugeln in Urne
Für die orangen Kugeln erhältst du folgende Verteilungsfunktion :
Gleiches gilt, wenn du die Verteilungsfunktion der türkisen Kugeln betrachtest:
Zeichnen wir diese beiden Verteilungsfunktionen nun in ein Diagramm ein, so erhalten wir folgendes Bild:
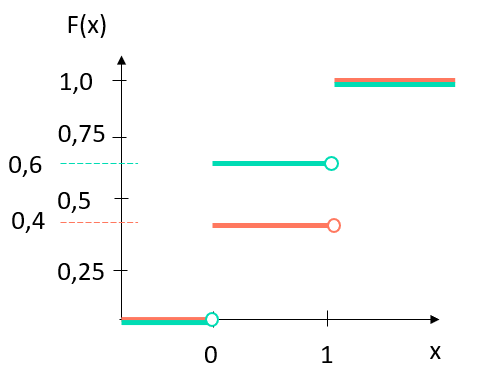
Abbildung 10: Verteilungsfunktion F(x) im Diagramm
Nachdem wir nun schon die Wahrscheinlichkeitsfunktion und die Verteilungsfunktion kennengelernt haben, tauchen wir noch ein wenig tiefer in das Thema ein. Nun beschäftigen wir uns nämlich noch mit ein paar Maßzahlen.
Bernoulli Verteilung – Erwartungswert
Der Erwartungswert E(X) spiegelt einen zukünftigen Mittelwert wider. Er nähert sich also einem bestimmten Erwartungswert E(X) an.
Der Erwartungswert E(X) einer Zufallsgröße X ist definiert durch:
Für den Erwartungswert E(X) einer Bernoulli-verteilten Zufallsgröße X gilt:
Warum erhalten wir im Falle des Bernoulli-Experiments als Erwartungswert ? Dies können wir ganz einfach überprüfen.
Der x-Wert kann lediglich die Werte 0 und 1 annehmen. Wir erhalten also für die Wahrscheinlichkeiten P:
In die Gleichung des Erwartungswertes eingesetzt, ergibt sich:
Berechnen wir den Erwartungswert E(X) für unser Urnenbeispiel.
Von den insgesamt 5 Kugeln sind 3 orange Kugeln dabei und 2 türkise Kugeln. Wir berechnen für beide den Erwartungswert E(X).
Die Trefferwahrscheinlichkeit p liegt bei:
Demnach erhalten wir für den Erwartungswert E(X) jeweils:
Orange:
Türkis:
Zuletzt sehen wir uns noch die Varianz Var(X) und die Standardabweichung zum Bernoulli-Experiment an.
Bernoulli Verteilung – Varianz und Standardabweichung
Wie du vielleicht schon weißt, ist die Varianz Var(X) ein Maß für die Streuung einer Zufallsgröße X. Mathematisch ist sie definiert durch:
Varianz Var(X) einer Zufallsgröße X:
Varianz Var(X) einer Bernoulli-verteilten Zufallsgröße X:
Wir versuchen wieder die neu entstandene Formel für eine Bernoulli-Verteilung aus der allgemeinen Formel herzuleiten.
Mögliche Werte für x, P und E(X) sind:
Wir setzen in die allgemeine Gleichung ein und lösen auf:
Nachdem wir die Formel für die Varianz Var(X) kennen, ist es ein leichtes noch die Standardabweichung herzuleiten, da für die Beziehung zwischen Standardabweichung und Varianz Var(X) gilt:
Nun müssen wir lediglich die Wurzel ziehen, um die Standardabweichung berechnen zu können. Wir definieren also:
Standardabweichung einer Bernoulli-verteilten Zufallsgröße X:
Da ein Bernoulli-Experiment immer nur zwei mögliche Ausgänge liefert, ist die Berechnung der Wahrscheinlichkeiten und die zugehörige Wahrscheinlichkeitsverteilung f(x) sowie die Verteilungsfunktion F(x) noch relativ einfach. Was aber, wenn wir den Versuch nicht nur einmal durchführen, sondern n-fach? Dann erhalten wir eine Bernoulli-Kette. Sehen wir uns diese noch einmal genauer an.
Wiederholung eines Bernoulli-Experiments (Bernoulli-Kette)
Wie bereits erwähnt, können wir ein Bernoulli-Experiment n-fach wiederholen. Dann handelt es sich um eine Bernoulli-Kette mit der Länge n. Zur Erklärung führen wir das Beispiel eines Münzwurfs von oben fort.
Wir haben die Münze bereits einmal geworfen und dabei die Wahrscheinlichkeit P ausgerechnet, mit der wir "Kopf" erhalten.

Wir werfen die Münze erneut. Wir führen also eine Bernoulli-Kette aus mit . Dieses Mal interessiert uns aber nicht nur, wie wahrscheinlich es ist Kopf oder Zahl zu werfen, sondern wie wahrscheinlich es ist sogar zweimal hintereinander Kopf zu werfen. Als Baumdiagramm lässt sich dies wieder wie folgt darstellen:
 Abbildung 11: Baumdiagramm Bernoulli-Kette
Abbildung 11: Baumdiagramm Bernoulli-Kette
Die Wahrscheinlichkeit P, mit der zweimal hintereinander Kopf geworfen wird, zeichnet sich durch den blauen Pfad aus. Berechnet werden kann sie durch Multiplikation der Trefferwahrscheinlichkeiten p entlang des Pfads. Es gilt:
Damit beträgt die Wahrscheinlichkeit P, zweimal hintereinander Kopf zu werfen, 25 %.
So eine Aufgabenstellung lässt sich noch relativ einfach lösen. Was aber, wenn es komplizierter wird? Müssen wir dazu jedes Mal ein Baumdiagramm zeichnen und die Wahrscheinlichkeiten entlang des Pfades ausrechnen? Nein, zum Glück nicht. Dazu gibt es einen einfacheren Weg.
Wir bedienen uns dazu dem Hilfsmittel des Binomialkoeffizienten . Damit lassen sich die Pfade eines Baumdiagramms, die zu einem bestimmten Ausgang führen, ermitteln.
Was genau es mit dem Binomialkoeffizienten auf sich hat, kannst du im entsprechenden Kapitel auf StudySmarter nachlesen.
Wahrscheinlichkeit für genau k Treffer mit einer Trefferwahrscheinlichkeit p einer Bernoulli-Kette der Länge n:
Die Zufallsgröße X gibt hierbei die Anzahl der Treffer k an. Wir sehen uns dazu gleich ein Beispiel an.
Eine Urne mit acht Kugeln enthält drei blaue Kugeln und fünf schwarze Kugeln. Es soll die Wahrscheinlichkeit ermittelt werden, bei fünf Ziehungen viermal eine blaue Kugel zu ziehen.
 Abbildung 12: Kugeln in Urne
Abbildung 12: Kugeln in Urne
Wie sollen wir vier blaue Kugeln ziehen, wenn wir doch nur drei blaue Kugeln haben? Das liegt daran, dass wir die Kugeln nach dem Ziehen wieder zurück in die Urne legen. Andernfalls würde sich die Trefferwahrscheinlichkeit p bei den Folgeversuchen ändern. Damit wäre es keine Bernoulli-Kette mehr.
Eine Bernoulli-Kette ist demnach ein Zufallsexperiment mit Zurücklegen, da die Trefferwahrscheinlichkeit konstant bleiben muss.
Bevor wir die Formel anwenden, definieren wir kurz die erforderlichen Werte dafür.
Nun setzen wir die Werte in die Formel von oben ein:
Die Wahrscheinlichkeit für das Ziehen von vier blauen Kugeln liegt demnach bei 6,2 %.
Hast du dich gefragt, wie sich diese Gleichung für die Wahrscheinlichkeit in den Taschenrechner eingeben lässt? Sieh dir dazu unsere Vertiefung an!
Binomialkoeffizienten in den Taschenrechner einzugeben, ist nicht schwer. Zum Glück erledigt der Taschenrechner den größten Teil für uns. Sehen wir uns einmal kurz an, was wir dazu machen müssen. Wir nehmen das Beispiel von oben mit:
Verwendet wurde für die Berechnung das Modell CASIO fx-991DEX.
Wir starten bei "MENU" und gehen auf "7: Verteilungsfkt.":
 Abbildung 13: Menü CASIO
Abbildung 13: Menü CASIO
Dort öffnet sich dann ein Untermenü, wobei wir "4: Binomial-Dichte" einstellen.
 Abbildung 14: Untermenü Verteilungsfunktionen
Abbildung 14: Untermenü Verteilungsfunktionen
Danach gibt es die Möglichkeit, die Werte über eine Liste einzugeben oder nur die Variablen. Wir wählen "2: Variable".
 Abbildung 15: Binomial-Verteilung Auswahl
Abbildung 15: Binomial-Verteilung Auswahl
Es erscheint eine Eingabemaske, bei der sich k, n und p eingeben lassen. Diese geben wir entsprechend der obigen Vorgaben ein.
 Abbildung 16: Eingabe Werte für Binomial-Dichte
Abbildung 16: Eingabe Werte für Binomial-Dichte
Mit Drücken auf die Ergebnistaste erhalten wir für die Wahrscheinlichkeit:
Für unser Beispiel der Bernoulli-Kette sehen wir uns noch kurz die Wahrscheinlichkeitsverteilung f(x) und die Verteilungsfunktion F(x) an.
Um die Wahrscheinlichkeitsverteilung f(x) in einem Histogramm einzeichnen zu können, benötigen wir die richtigen Werte. Dazu erstellen wir eine Tabelle. Am einfachsten lässt sich das über die Listenfunktion des Taschenrechners realisieren.
| k | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 0,095 | 0,286 | 0,343 | 0,206 | 0,062 | 0,007 |
Jetzt nur noch in ein Histogramm einzeichnen und wir erhalten:
 Abbildung 17: Wahrscheinlichkeitsverteilung im Histogramm
Abbildung 17: Wahrscheinlichkeitsverteilung im Histogramm
Ist dir etwas aufgefallen? Das entstandene Histogramm sieht stark nach einer Binomialverteilung aus! Die Zufallsgröße X einer Bernoulli-Kette ist also binomialverteilt.
Der Vollständigkeit halber wollen wir ebenfalls noch die Verteilungsfunktion F(x) zeichnen. Wir erstellen dazu wieder eine Tabelle mithilfe des Taschenrechners.
| k | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 0,095 | 0,381 | 0,725 | 0,931 | 0,993 | 1 |
Eingezeichnet in ein Diagramm ergibt sich folgendes Bild:
 Abbildung 18: Verteilungsfunktion im Diagramm
Abbildung 18: Verteilungsfunktion im Diagramm
Fassen wir die Ergebnisse unseres Beispiels noch einmal allgemein zusammen:
Die Zufallsgröße X einer n-fachen Wiederholung eines Bernoulli-Experiments (Bernoulli-Kette) wird als binomialverteilt bezeichnet.
Die Bernoulli-Verteilung ist somit ein Spezialfall der Binomialverteilung mit .
Bernoulli Verteilung - Das Wichtigste
- Ein Bernoulli Experiment ist ein Zufallsexperiment mit nur zwei möglichen Ausgängen (Erfolg und Misserfolg).
- Die n-fache Wiederholung eines Bernoulli-Experiments führt zu einer Bernoulli-Kette und ist binomialverteilt.
- Die Bernoulli-Verteilung ist demnach ein Spezialfall der Binomialverteilung mit .
- Es ergeben sich die Wahrscheinlichkeiten eines Erfolgs/Misserfolgs des Bernoulli-Experiments mit:
- (Erfolg)
- (Misserfolg).
- Die Wahrscheinlichkeitsverteilung f(x) eines Bernoulli-Experiments lautet:
-
- Möglich ist die Darstellung als Funktionsgraph, in einem Stabdiagramm und in einem Histogramm.
- Für die Verteilungsfunktion F(x) eines Bernoulli-Experiments gilt:
- Der Erwartungswert E(X) der Bernoulli-verteilten Zufallsgröße X ist: .
- Die zugehörige Varianz Var(X) und Standardabweichung sind:
- Die Wahrscheinlichkeit für genau k Treffer einer Bernoulli-Kette der Länge n mit der Trefferwahrscheinlichkeit p ist:
Verwandte Themen zu Stochastik
Wie stellen wir sicher, dass unser Content korrekt und vertrauenswürdig ist?
Bei StudySmarter haben wir eine Lernplattform geschaffen, die Millionen von Studierende unterstützt. Lerne die Menschen kennen, die hart daran arbeiten, Fakten basierten Content zu liefern und sicherzustellen, dass er überprüft wird.
Content-Erstellungsprozess:
Lily Hulatt ist Digital Content Specialist mit über drei Jahren Erfahrung in Content-Strategie und Curriculum-Design. Sie hat 2022 ihren Doktortitel in Englischer Literatur an der Durham University erhalten, dort auch im Fachbereich Englische Studien unterrichtet und an verschiedenen Veröffentlichungen mitgewirkt. Lily ist Expertin für Englische Literatur, Englische Sprache, Geschichte und Philosophie.
Lerne Lily
kennen
Inhaltliche Qualität geprüft von:
Gabriel Freitas ist AI Engineer mit solider Erfahrung in Softwareentwicklung, maschinellen Lernalgorithmen und generativer KI, einschließlich Anwendungen großer Sprachmodelle (LLMs). Er hat Elektrotechnik an der Universität von São Paulo studiert und macht aktuell seinen MSc in Computertechnik an der Universität von Campinas mit Schwerpunkt auf maschinellem Lernen. Gabriel hat einen starken Hintergrund in Software-Engineering und hat an Projekten zu Computer Vision, Embedded AI und LLM-Anwendungen gearbeitet.
Lerne Gabriel
kennen




























